• False Position Method

Bisection method for the equation x3−2x−2 = 0 which has a single root between x=−4 and x = 2. Here's the code I have program bisection2. Bisection method in fortran 90 Physics Forums. All the Fortran 90 programs listed here are corresponding to the Fortran 77 programs appeared in or related to the book. Several programs (as indicated) have appeared in the book, which are copyrighted by Cambridge University Press. Some changes are made in order to take advantage of Fortran 90. F2c (GNU Fortran to C translator, dmg@bell-labs.com) C2F (C to Fortran translator, David Frank) Sun WorkShop Developer Products Try & Buy Evaluation Program (compilers free for 30 days) The f77 Problem Page (f77reorder, Wolfgang Wander) Elf90 (free F90 subset from Lahey for DOS/Windows) diagram.for (Simple Diagrammer for Fortran Language Programs).

Bisection method is used to find the real roots of a nonlinear equation. The process is based on the ‘‘. According to the theorem “If a function f(x)=0 is continuous in an interval (a,b), such that f(a) and f(b) are of opposite nature or opposite signs, then there exists at least one or an odd number of roots between a and b.” In this post, the algorithm and flowchart for bisection method has been presented along with its salient features. Bisection method is a closed bracket method and requires two initial guesses. It is the simplest method with slow but steady rate of convergence. It never fails! The overall accuracy obtained is very good, so it is more reliable in comparison to the or the.

Features of Bisection Method. Type – closed bracket. No. Of initial guesses – 2. Convergence – linear. Rate of convergence – slow but steady.

False Position Method

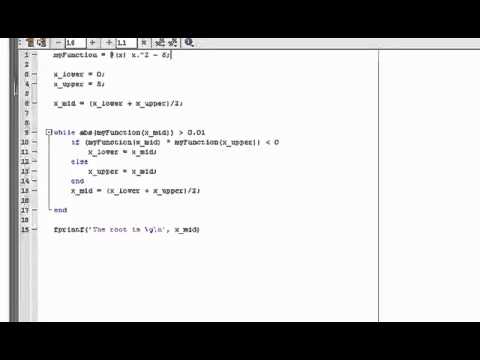
Accuracy – good. Programming effort – easy. Approach – middle point Bisection Method Algorithm:. Start. Read x1, x2, e.Here x1 and x2 are initial guesses e is the absolute error i.e. The desired degree of accuracy.

Compute: f1 = f(x1) and f2 = f(x2). If (f1.f2) 0, then display initial guesses are wrong and goto (11). Otherwise continue. x = (x1 + x2)/2. If ( (x1 – x2)/x 0), then x1 = x and f1 = f. Else, x2 = x and f2 = f.Now the loop continues with new values.

Stop Bisection Method Flowchart: The algorithm and flowchart presented above can be used to understand how bisection method works and to write program for bisection method in any programming language. Also see, Note: Bisection method guarantees the convergence of a function f(x) if it is continuous on the interval a,b (denoted by x1 and x2 in the above algorithm. For this, f(a) and f(b) should be of opposite nature i.e. Opposite signs. The slow convergence in bisection method is due to the fact that the absolute error is halved at each step. Due to this the method undergoes linear convergence, which is comparatively slower than the Newton-Raphson method, Secant method and False Position method.

Here are the Bisection Method formulas xm = (xl+xu)/2 I'm not convinced that you understand what the above means. X L - Lower (left) endpoint of an interval x M - Midpoint of an interval x U - Upper (right) endpoint of an interval a) If f(x L).f(x M) 0, the graph of the function does not cross the x-axis between x L and x M, so we should look in the other half of the interval - in x M, x U. If so, USE THE SAME VALUE FOR x U (i.e., don't change x U), but reset x L to x M. Your code should NOT include x U = x U. At each step for a) or b), we are shortening the interval by half its length, so that we eventually find the root. C) If f(x L).f(x M) = 0 then either f(x L) = 0 or f(x M). There's probably an assumption that f(x L) ≠ 0 and f(x U) ≠ 0, but you didn't show it in the attachment you posted.